Quadratic functions are essential in mathematics and are often studied in algebra courses. Understanding transformations with quadratic functions is crucial for mastering this topic. A transformations worksheet can help students practice and reinforce their knowledge of how quadratic functions can be shifted, stretched, and flipped.
By working on a transformations worksheet, students can visualize how changes to the coefficients of a quadratic function affect its graph. This hands-on approach allows them to see the direct impact of each transformation and gain a deeper understanding of how these functions behave.
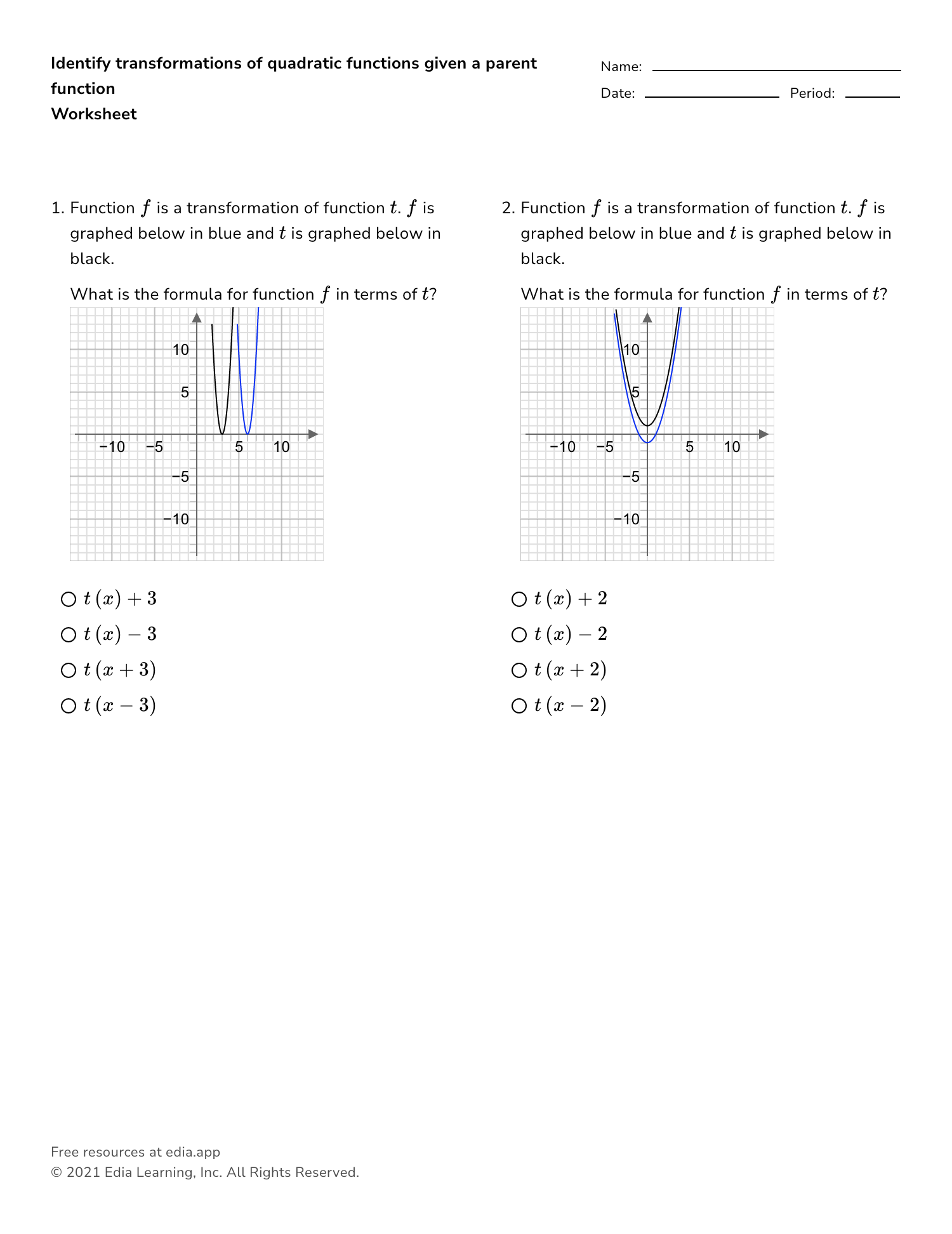
Transformations with Quadratic Functions Worksheet
One common transformation of quadratic functions is a vertical shift, where the entire graph is moved up or down. This can be achieved by adding or subtracting a constant term to the function. Students can practice identifying the effects of vertical shifts on a transformations worksheet, helping them grasp this concept more effectively.
Another transformation is a horizontal shift, which involves moving the graph left or right. This can be done by replacing the variable x with (x – h), where h represents the horizontal shift. By completing exercises on horizontal shifts on a worksheet, students can improve their skills in recognizing and applying this transformation.
In addition to shifts, quadratic functions can also undergo stretches or compressions. These transformations alter the width of the graph and can be achieved by multiplying the function by a constant greater than 1 for stretches or between 0 and 1 for compressions. Practicing stretches and compressions on a worksheet can help students understand how these transformations affect the shape of the graph.
Furthermore, students can explore reflections of quadratic functions across the x-axis or y-axis. These transformations involve changing the sign of the function or its variable. By completing reflection exercises on a worksheet, students can enhance their ability to identify and apply these transformations accurately.
In conclusion, a transformations worksheet for quadratic functions is a valuable tool for students to strengthen their understanding of how these functions can be altered. By practicing vertical shifts, horizontal shifts, stretches, compressions, and reflections, students can enhance their skills in graphing and analyzing quadratic functions. Through hands-on exercises and visual representations, students can master transformations with quadratic functions and excel in their algebra studies.